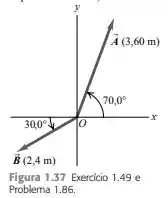
a) Escreva cada vetor indicado na Figura 1.37 em termos dos vetores unitários i e j. b) Use os vetores unitários para escrever o vetor C, onde C=3a - 4b. c) Encontre o módulo e a direção de C.
Passo 1
Faala ae, beleza??

Nesse problema queremos encontrar as componentes dos vetores e , obter o vetor de modo que .
Tem ideia de como fazemos isso? 🤔
Para obter os componentes dos vetores fazemos
Onde é o ângulo do vetor com o semi eixo poisito de
Veja só! 😉
Passo 2
Primeiro, vamos decompor os vetores em suas componentes. Então, temos que o tem tamanho e faz com o eixo . Assim, podemos montar o triângulo com suas componentes:
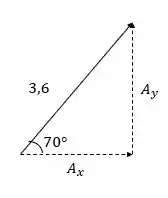
Assim, podemos achar as componentes fazendo:
Com isso:
Tranquilo até aqui? 👀
Passo 3
Vamos fazer a mesma coisa para o , beleza? Então, temos o seguinte triângulo:
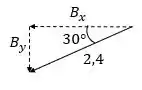
Dessa forma:
Com isso:
Bacana, não é? 😎
Passo 4
Show!! Agora, vamos achar , fazendor:
Então:
Juntando as componentes dos mesmos vetores unitários:
Beleza?
Passo 5
Agora, vamos achar o módulo e a direção de . Para isso, temos que o módulo será:
Já para a direção, precisamos saber seu ângulo em relção ao eixo positivo.
Para isso, vamos utilizar a relação:
E sabemos que:
Então:
Isso, em relação ao eixo positivo, no sentido anti-horário.
Ok?? Só isso! O que achou? Responde Aí! 😊

Resposta
a) ; .
b) .
c) ;.